Kinematika merupakan suatu ilmu yang mempelajari sistematika gerak atau bagaimana gerak tersebut terjadi dimana penyebab terjadinya gerakan tersebut tidak dianggap atau tidak diperdulikan. Kinematika terdiri dari Gerak lurus yang mencakup Gerak Lurus Beraturan (GLB) dan Gerak Lurus Berubah Beraturan (GLBB). Gerak Melingkar Beraturan dan Perpaduan Gerak
1. Gerak Lurus
Gerak benda pada lintasan lurus disebut dengan gerak lurus. Ada dua macam Gerak lurus, yaitu gerak lurus beraturan dan gerak lurus berubah beraturan.
- Gerak Lurus Beraturan (GLB)
Gerak lurus beraturan adalah gerak benda pada lintasan lurus dengan kecepatan konstan atau tetap. Secara umum rumus persamaan GLB yaitu sebagai berikut :
v = Kecepatan (m/s)
s = Jarak (m)
t = Waktu (s)
- Gerak Lurus Berubah Beraturan
Gerak lurus berubah beraturan adalah gerak benda pada lintasan lurus dengan kecepatan berubah secara beraturan yang dikarenakan mengalami percepatan tetap. Rumus persamaan dalam gerak lurus berubah beraturan sebagai berikut :
Jika disajikan dalam grafik kecepatan v terhadap waktu t, maka:
Sehingga s = Luas Kurva
Kecepatan Sesaat
vt = kecepatan akhir (m/s)
v0= Kecepatan awal (m/s)
a = Percepatan (m/s^2)
s = Jarak (m)
t = Waktu (s)
Aplikasi dari persamaan GLBB dapat digunakan pada gerak jatuh bebas, gerak vertikal ke atas maupun vertikal ke bawah.
Gerak Jatuh Bebas
Pada gerak jatuh bebas v0 = 0 sehingga kecepatan dan waktu benda mencapai tanah dapat dirumuskan dengan persamaan berikut :
Vt = Kecepatan saat t sekon (m/s)
h = Jarak yang ditempuh benda (m)
g = percepatan gravitasi (9,8 m/s^2)
t = waktu (s)
Gerak Vertikal ke Atas
Kecepatan awal v0 arah ke atas
Gerak Vertikal ke Bawah
Kecepatan awal v0 arah ke bawah
g =Percepatan gravitasi bumi (10m/s^2)
ht = Ketinggian benda akhir (m)
h0 = Ketinggian benda mula-mula (m)
2. Gerak Melingkar Beraturan (GMB)
Gerak melingkar beraturan (GMB) dapat didefinisikan sebagai gerak benda pada lintasan berupa lingkaran dengan kecepatan sudut tetap. Dalam gerak melingkar beraturan, ada beberapa istilah sebagai berikut:
- Frekuensi dan Periode
Frekuensi adalah banyaknya putaran dalam tiap detik sedangkan periode adalah waktu yang diperlukan untuk berotasi satu putaran. Secara matematis besarnya frekuensi dan periode dapat dinyatakan dalam rumus persamaan berikut :
Frekuensi :
Periode :
f = Frekuensi (Hz)
n = Jumlah putaran
t = Waktu (s)
T = Periode - Kecepatan Sudut
Kecepatan sudut adalah besarnya sudut yang ditempuh tiap satuan waktu. Rumus persamaan kecepatan sudut dapat dinyatakan sebagai berikut :
v = Kecepatan linier (m/s)
R = Jari-jari lintasan (m)
Beberapa satuan dari kecepatan sudut, diantaranya :
1 putaran/sekon =
1 rps (rotasi per sekon) =
1 rpm (rotasi per menit) =
- Percepatan Sentripetal
Percepatan sentripetal adalah percepatan benda terjadi pada benda bergerak melingkar beraturan yang memiliki arah menuju ke pusat. Besarnya percepatan sentripetal dapat dinyatakan dalam rumus persamaan berikut :
Satu sumbu putar
v = Kecepatan linier (m/s)
R = Jari-jari roda (m)
3. Perpaduan Gerak
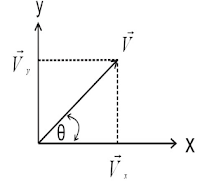
Kecepatan merupakan besaran vektor yang memiliki arah sehingga gerak benda dapat dipadukan jika benda bergerak dengan arah kecepatan yang berbeda seperti pada gambar
Sehingga dapat dituliskan dalam persamaan :
v = Resultan kecepatan (m/s)
Vx = Kecepatan benda terhadap sumbu x (m/s)
Vy = Kecepatan benda terhadap sumbu y (m/s)
Ada beberapa penerapan perpaduan gerak antara lain sebagai berikut :
- Gerak Parabola
Gerak parabola merupakan perpaduan antara gerak lurus beraturan (GLB) terhadap sumbu x dan gerak lurus berubah beraturan (GLBB) terhadap sumbu y.
Posisi Sesaat
Ketinggian Maksimum di B
Ketinggian Maksimum (h maks)
Waktu hingga ketinggian maksimum (
Jarak maksimum (R)
Waktu mencapai tanah kembali (
g = Percepatan gravitasi (m/s^2)
t = Waktu (s)
R = Jarak maksimum (m)